
"Si no puedes explicarlo de forma sencilla, no lo entiendes lo suficientemente bien" (Albert Einstein).

geo
"Si no puedes explicarlo de forma sencilla, no lo entiendes lo suficientemente bien" (Albert Einstein).
¿Qué significa que el suelo tiene un comportamiento no lineal?
La no-linealidad del suelo es un concepto fundamental en Ingeniería Geotécnica. Sin embargo, en la práctica asociada a proyectos rutinarios de fundaciones y muros, muchas veces no se considera este comportamiento en la estimación de parámetros geomecánicos a ser utilizados en modelos para predecir las deformaciones del sistema estructura-terreno ¿Quieres aprender algunos conceptos clave relacionados al comportamiento no lineal del terreno y su aplicación en la Ingeniería Geotécnica práctica? Continúa leyendo este post…
Contenido
Comportamiento no lineal del terreno
Uno de los principales problemas de la ingeniería de suelos es la aparente diferencia entre la rigidez de los suelos medida en ensayos de laboratorio y la calculada a partir de observaciones de los movimientos del terreno, tal como lo reportaron oportunamente numerosos investigadores en los últimos 50 años (Cole y Burland, 1972; St John, 1975; Wroth, 1975; Burland, 1979; Jardine et al, 1985; Cox & Mayne, 2015, por mencionar algunos). En la actualidad, estas diferencias se han conciliado, en gran medida gracias a la comprensión de las principales características de la rigidez del suelo y, en particular, a la importantísima influencia de la no linealidad.
Pero, ¿qué significa que el suelo tiene un comportamiento no lineal? Para poder comprender este concepto, es necesario revisar la Figura 1, tomada del trabajo de Mair (1993).
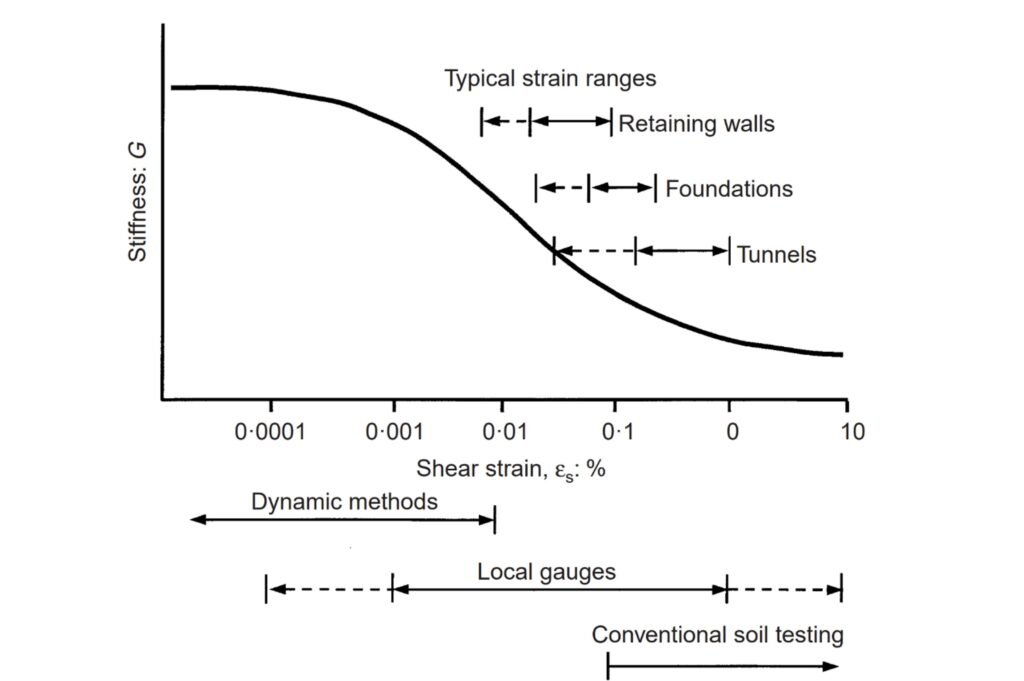
Figura 1 Comportamiento no lineal del suelo (Fuente: Mair, 1993).
En esta figura se muestra una curva rigidez-deformación típica de un suelo. Como puede observarse, a pequeñas deformaciones la rigidez (denotada por el módulo de corte G) es relativamente grande, mientras que para deformaciones cercanas a la falla, la rigidez es baja. De acuerdo a esto, es evidente que la rigidez del suelo no es constante, y que, además, depende del nivel de deformaciones. Estas son las dos características intrínsecamente ligadas a la no-linealidad del terreno.
¿Cómo se relaciona esta curva con una fundación de una estructura? Básicamente, considerando la premisa práctica básica según la cual, en general, las deformaciones en el suelo variarán desde cero, en un punto situado lejos de la estructura (a relativamente grandes profundidades), hasta valores relativamente grandes cerca de la misma, alcanzando valores importantes en el borde de una fundación rígida. Es decir, que los esfuerzos transmitidos por la estructura a diferentes profundidades, contribuirán de manera diferente a la movilización de las deformaciones y, por ende, el terreno se caracterizará por desarrollar diferentes niveles de rigidez.
Características de la no-linealidad del terreno
A fin de ahondar un poco en las características asociadas al comportamiento no-lineal del suelo, vamos a valernos de la Figura 2, tomada, esta vez, del texto de Atkinson (2007), y modificada para este post.
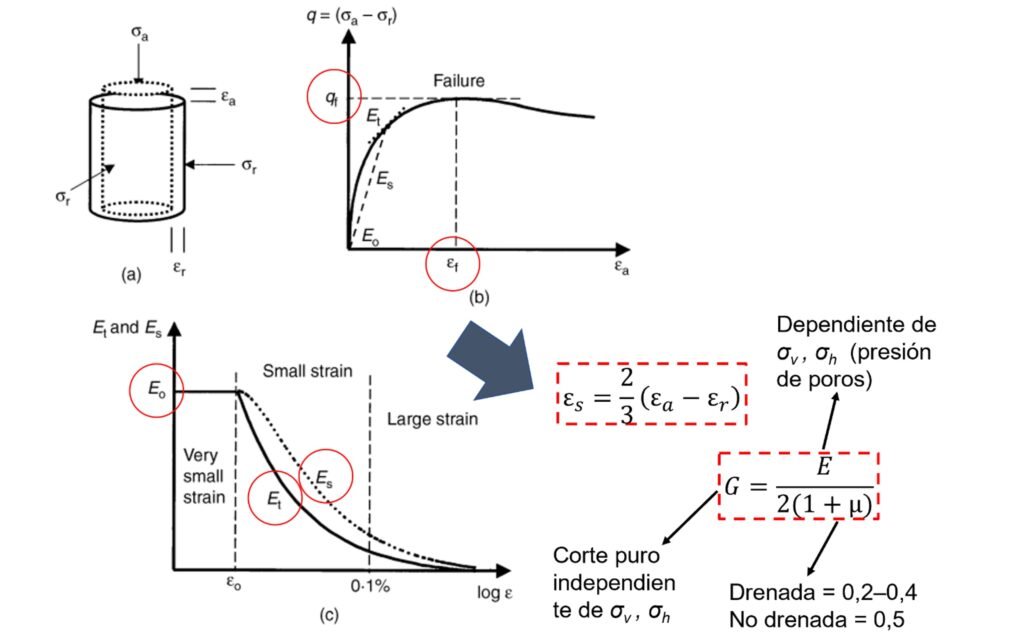
Figura 2 Parámetros de rigidez para un suelo no-lineal (Fuente: modificada de Atkinson, 2007).
Esta figura muestra los parámetros de esfuerzo-deformación básicos para una prueba triaxial. En la parte (a) de la figura, se observa una muestra cilíndrica sometida a esfuerzos axial (σa) y radial (σr), con las correspondientes deformaciones axial (εa) y radial (εr). Al ser cargada, se tiene una curva esfuerzo-deformación no-lineal, como la que se muestra en la parte (b) de la figura. La muestra falla en el esfuerzo desviador pico (qf) a una cierta deformación final (εf). En la figura se define también el módulo de deformación E, el cual puede ser tangente (Et) o secante (Es). La rigidez a muy pequeñas deformaciones, por su parte, está definida por el módulo inicial (Eo). Los módulos Et y Es varían con la deformación, como puede observarse en la parte (c) de la figura.
En esta parte (c) se definen tres regiones: la primera, correspondiente a muy pequeñas deformaciones (en la cual Et = Es = Eo), que se extiende hasta una deformación εo; la segunda, en la que los módulos comienzan a decaer desde εo hasta una deformación de alrededor de 0,1%; y la tercera, que corresponde a deformaciones superiores a 0,1%, en la cual la rigidez es relativamente pequeña.
Otro punto importante a destacar es la vinculación que existe entre el módulo de deformación E y el módulo de corte G, los cuales se relacionan mediante la expresión que se muestra en la figura anterior, según la Teoría de la Elasticidad. En la misma figura se muestra también la importante relación entre la deformación por corte εs y las deformaciones axial εa y radial (εr), típicamente medidas en ensayos de laboratorio.
Algo muy importante a destacar es que el módulo G tiene la particularidad de ser independiente de la presión de poros, y por ende G refleja el comportamiento del suelo en corte, independientemente de si el esfuerzo es efectivo o total. Este hecho es fundamental, porque implica que G puede ser empleado para la solución de problemas geotécnicos bajo condiciones estáticas, dado que, como han demostrado numerosos investigadores, la magnitud de la deformación (y no la velocidad de la deformación) es la que presenta mayor influencia en la rigidez del terreno.
Esto puede sonar raro para la mayoría de los Ingenieros Geotécnicos, porque, de alguna manera, hemos estado acostumbrados a emplear el módulo de corte únicamente para problemas dinámicos. Pero, como acabo de mencionar, el módulo G representa mejor la rigidez del terreno.
Comprender este comportamiento brevemente descrito en estas líneas es de suma importancia, porque nos dice que la rigidez del suelo no es única, y que, además, depende del estado de esfuerzos y de las deformaciones.
La no-linealidad del terreno en aplicaciones rutinarias
Usualmente, el análisis detallado y el diseño de una estructura geotécnica de envergadura requerirán la realización de ensayos de laboratorio especiales, que impliquen la aplicación de trayectorias de esfuerzos complejas y la medición de pequeñas deformaciones, junto con análisis numéricos que utilicen modelos constitutivos que consideren las características importantes del comportamiento del suelo (Atkinson, 2000).
Sin embargo, hay muchos casos en los que no es necesario disponer de análisis tan detallados, y en los que sólo se necesitan soluciones relativamente sencillas. Estos son los que yo llamo “proyectos geotécnicos rutinarios”, como pueden ser muros o edificaciones convencionales, casas unifamiliares o multifamiliares, piscinas y tanques subterráneos, entre otros, considerando la presencia de suelos sedimentarios que no presenten características especiales (como podría ser la propiedad de expandir o colapsar ante la presencia de agua, por mencionar solo dos de estas características).
La figura 3 ilustra el asentamiento de una cimentación superficial cargada y los dos métodos principales para su diseño rutinario, cuyos principios generales aplican también al diseño y análisis de muros de contención simples e, incluso, túneles, como ya hemos revisado anteriormente en otro post (ver https://geo-webonline.com/comportamiento-de-fundaciones-superficiales/).
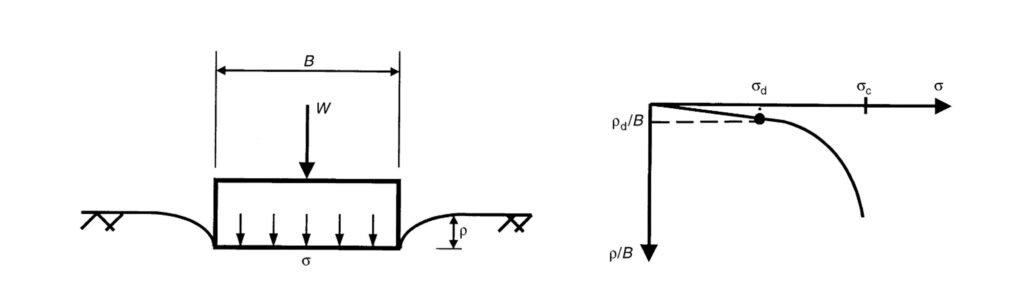
Figura 3 Comportamiento de fundaciones en proyectos rutinarios (Fuente: modificado de Atkinson, 2007).
Para la cimentación superficial mostrada en la figura, el requisito básico es determinar la presión de apoyo de diseño σd que causará un asentamiento de diseño ρd. Para estimar la presión de apoyo admisible σa, se emplea una expresión que tiene la forma de la ecuación mostrada a continuación:
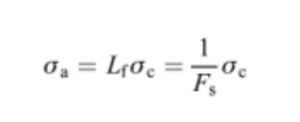
donde σc es una capacidad portante última calculada, Lf es un factor de carga y Fs es un factor de seguridad, siendo Fs = 1/Lf . En este método, el factor de seguridad o factor de carga está ahí para limitar los asentamientos, es decir, que busca reducir la capacidad portante última en un factor dado, de manera que el punto de diseño esté en la parte de la curva de carga-asentamiento en el que los asentamientos son relativamente pequeños.
El asentamiento, por su parte, viene dado por una expresión del tipo:

donde Δρ es el cambio de asentamiento debido a un cambio de presión de apoyo Δσ, B es el ancho de la cimentación, μ es la relación de Poisson, Iρ es un factor de influencia que depende principalmente de la geometría de la cimentación (Poulos & Davis, 1974), y Es es el módulo de Young secante correspondiente al incremento de carga. El parámetro Es puede relacionarse con el módulo de Young para deformaciones muy pequeñas Eo a través de una relación de rigidez Es/Eo.
De acuerdo a lo anterior, resulta importante mencionar que el factor de carga Lf y la relación de rigidez Es/Eo son parámetros de diseño, los cuales dependerán, entre otras cosas, del suelo, de su estado y de su comportamiento esfuerzo-deformación, de la estructura, y de los movimientos de diseño (es decir, de las deformaciones asumidas para el diseño). Dado que estos sencillos métodos rutinarios de diseño sólo pretenden determinar un movimiento, siempre debe ser posible seleccionar factores de carga o relaciones de rigidez que ofrezcan soluciones correctas.
De acuerdo a esto, para seleccionar el valor de G y, posteriormente, el de Es, el problema radica en conocer cuál es el nivel de deformaciones aproximado del terreno cuando éste sea solicitado por la estructura, considerando que ese, justamente, es el objetivo de la estimación de asentamientos o deformaciones en cualquier proyecto geotécnico. Algo realmente paradójico.
¿Cómo se soluciona el problema? Aplicando, como en muchas otras áreas de la ciencia, la observación y las estadísticas de los datos observados. Si regresamos a la Figura 1, verán que en la misma se señalan rangos típicos de deformaciones para diferentes estructuras. Estos rangos se basan en observaciones y mediciones realizadas en numerosos proyectos a lo largo de los años.
Así, de acuerdo a esta gráfica, disponemos de un dato importante para el diseño de, por ejemplo, una fundación o un muro: vemos que la deformación típica para fundaciones superficiales y muros está en el orden del 0,1%. Este valor, para que tengan una idea, representa un movimiento de aproximadamente 10 mm en un estrato deformable de 10 m de espesor, tal como vemos en la Figura 4.
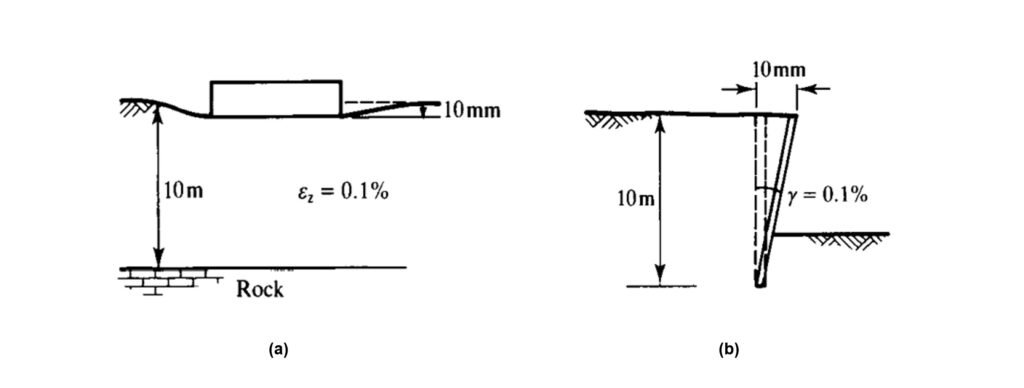
Figura 4 Niveles de deformación típicos para: (a) cimentaciones superficiales y (b) muros (Fuente: modificado de Atkinson, 2007).
Para cerrar, creo importante destacar que estos métodos simples son, por supuesto, limitados. Sólo sirven para estimar un movimiento en una dirección para estructuras relativamente sencillas y suelos con buen comportamiento. Si se necesita más información, como los movimientos verticales y horizontales o un pronóstico de los asentamientos o la distribución de los esfueros en el suelo, será necesario realizar análisis mucho más complejos.
Otro aspecto importante es cómo determinar la curva de variación de G con la deformación. Existen varias metodologías para ello, incluso normalizadas, como la establecida en el EUROCODIGO 7. Pero ese es un tema que trataremos en un próximo post…
Referencias
- Atkinson, J. H. (2000) “No-lineal Soil Stiffness in Routine Design”. Geotechnique 50, No. 5, 487-508.
- Atkinson, J. (2007) “The Mechanics of Soils and Foundations”. Second Edition. CRC Press – Taylor & Francis Group. Abingdon, UK.
- Jardine, R.; Fourie, A.; Maswoswe, J. & Burland, J. (1985) “Field and Laboratory Measurements of Soil Stiffness”. Proceedings of the Eleventh International Conference on Soil Mechanics and Foundation Engineering, pp. 511-514. San Francisco, USA.
- Mitchell, J.K. & Soga, K. (2005) “Fundamentals of Soil Behavior”. Third Edition. John Wiley & Sons, Inc. New Jersey, USA.