

Uso del módulo de corte “G” en análisis de asentamientos de cimentaciones bajo cargas estáticas
Tradicionalmente, en Ingeniería Geotécnica se ha empleado el módulo de deformación E para la estimación de asentamientos en cimentaciones bajo cargas estáticas. Sin embargo, si se considera el comportamiento mecánico del terreno, el empleo del módulo de corte G resulta más conveniente, aún cuando no sea frecuente su uso para este tipo de análisis ¿Quieres aprender más sobre este tema? Continúa leyendo este post…
Contenido
Comportamiento mecánico de un material
A fin de comprender lo relacionado al empleo del módulo de corte G en la estimación de asentamientos bajo cargas estáticas, primeramente echaremos un vistazo al comportamiento mecánico de un material, de manera de reconocer ciertos conceptos básicos.
Para un material dado, la relación entre esfuerzos y deformaciones está regida, como resulta lógico de suponer, por sus propiedades. Así, ante la presencia de un material idealmente rígido, las deformaciones serían nulas y los movimientos sólo podrían ocurrir si existiese un mecanismo que lo genere. Para materiales reales, ocurre que los mismos pueden comprimirse (o estirarse) o deformarse, tal como se muestra en la Figura 1, tomada del texto de Atkinson (2007).
La parte (a) de la figura muestra un bloque de material sometido a una presión de confinamiento σ y la parte (c) muestra una relación entre dicha presión y el cambio de volumen, cuyo gradiente es el módulo volumétrico K. Según se observa en esta gráfica, el esfuerzo puede aumentarse más o menos indefinidamente, y el material seguirá comprimiéndose de forma estable sin alcanzar la falla, mientras que el módulo K sigue aumentando con el esfuerzo y la deformación.
Por otro lado, la parte (b) de la Figura 1 muestra un bloque de material sometido a esfuerzos de corte τ, lo cual genera que se deforme al cortarse. La parte (d) ilustra una relación simple entre el esfuerzo cortante y la deformación por corte, según la cual el gradiente es el módulo de corte G, que se reduce con el esfuerzo y la deformación. Así, el material falla cuando no puede añadirse más esfuerzo de corte y continúa deformándose a un esfuerzo de corte constante τf, que representa la resistencia al corte del material.
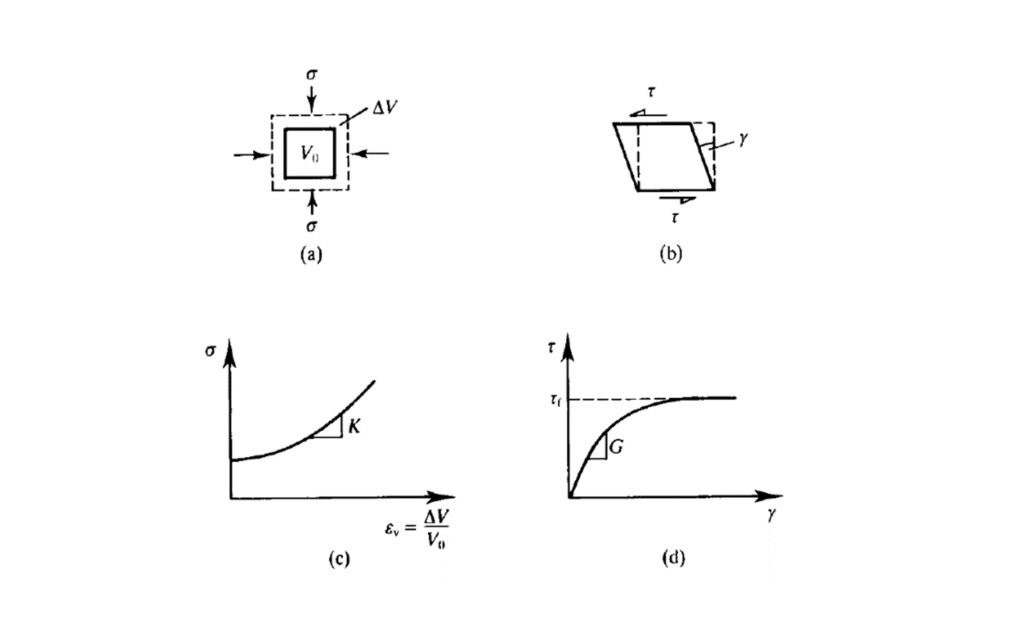
Figura 1 Compresión y distorsión de un material (Fuente: Atkinson, 2007).
Tal como se desprende de la figura que estamos analizando, la compresión observada en la parte (a) implica un cambio de tamaño, mientras que la distorsión por corte de la parte (b) implica un cambio de forma.
En general, en cualquier material (y, por ende, también en el suelo) sometido a carga, la compresión y la distorsión se producen de manera simultánea. Es por ello que la rigidez del material relaciona los cambios de esfuerzos y los cambios de deformación mediante las siguientes expresiones, basadas en las gráficas de la Figura 1:
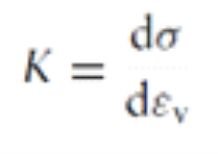
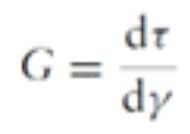
donde εv = V/Vo es la deformación volumétrica y γ es la deformación por corte. La teoría más sencilla de la rigidez es la Teoría de la Elasticidad, en la que K y G son constantes y se aplican por igual a la carga y a la descarga.
Selección de parámetros de rigidez del terreno
En Ingeniería Geotécnica, la selección de los parámetros de rigidez del terreno depende tanto de las condiciones de drenaje (es decir, de si el suelo podría o no sufrir cambios de volumen), como del nivel de deformaciones (Simons & Menzies, 2000).
En el caso del módulo de Young E, cuando se considera bajo condiciones drenadas o efectivas (denotado típicamente como E´), este parámetro incorpora tanto las deformaciones volumétricas como las deformaciones por corte. Sin embargo, cuando se considera bajo condiciones no drenadas o de esfuerzos totales (denotado como Eu), únicamente incorpora las deformaciones por corte, sin considerar cambios de volumen.
En este contexto, el empleo del módulo de Young como parámetro de rigidez del suelo resulta atractiva desde el punto de vista práctico, fundamentalmente porque es un concepto relativamente fácil de comprender a partir de una curva esfuerzo-deformación; y porque puede obtenerse a partir de ensayos de laboratorio relativamente sencillos (aunque no necesariamente con un nivel de precisión adecuado respecto a las condiciones in situ).
Sin embargo, en base a los conceptos mecánicos repasados en la sección anterior, una mejor aproximación al problema de establecer la rigidez del terreno incluye el empleo del módulo volumétrico K y del módulo de corte G, lo cual permitiría separar la deformación del suelo en dos componentes: la volumétrica (que implica un cambio de tamaño sin deformación por corte), y la distorsiva (asociada a un cambio de forma a volumen constante).
Un hecho de suma importancia a destacar es que el módulo de corte G es independiente de las condiciones de drenaje, lo cual significa que, en términos de análisis numéricos, cuando las condiciones de carga pasan de un estado no drenado a un estado drenado, G permanece constante, mientras que E debe adaptarse desde Eu a E´ (Matthews et al, 1996).
La variación típica del módulo de corte G con la deformación para la mayoría de los suelos se muestra en la Figura 2. Según esta figura, es evidente que el suelo tiene un comportamiento no lineal, tal como se ha explicado en un post anterior (ver https://geo-webonline.com/que-significa-que-el-suelo-tiene-un-comportamiento-no-lineal/).
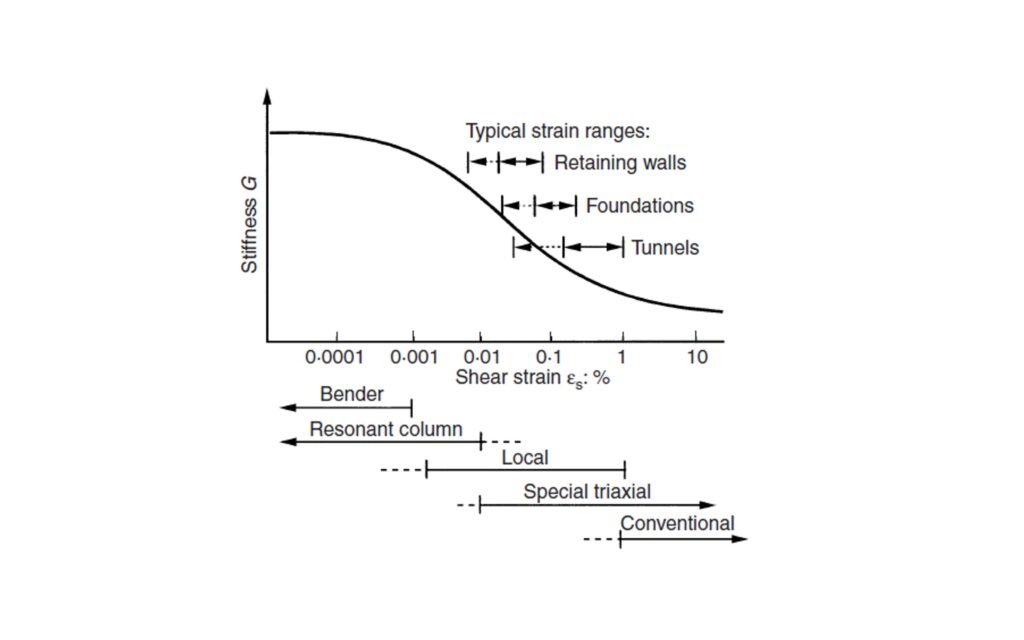
Figura 2 Variación de la rigidez con la deformación (Fuente: Simons & Menzies, 2000).
Existen numerosas metodologías prácticas para construir la curva de rigidez de un suelo dado, algunas de las cuales están, incluso, normalizadas (ver, por ejemplo, el EUROCÓDIGO 7). Usualmente, se determina experimentalmente el valor de Go correspondiente a muy pequeñas deformaciones, y a partir de ahí el resto de la curva. Un detalle importante es que Go puede ser determinado a partir de ensayos geofísicos in situ (como el down-hole, por ejemplo), lo cual resulta en una enorme ventaja costo-beneficio para el proyecto.
Volviendo a la figura, se observa que una deformación típica característica del terreno para fundaciones es de alrededor de 0,1%, valor que equivale a un asentamiento de la fundación del orden de 10 mm en un perfil compresible de 10 m de profundidad (Mair, 1993; Atkinson, 2007).
Así, conocida la curva de variación de G vs γ, es posible estimar valores de G correspondientes a las deformaciones esperadas para una estructura dada, y estimar posteriormente el valor de E´ (típicamente requerido en los modelos disponibles para la estimación de asentamientos) a partir de la siguiente expresión, propuesta por la Teoría de la Elasticidad:
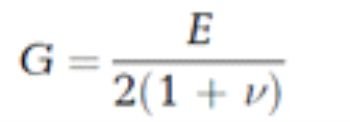
Sin embargo, surge un interrogante muy común en la práctica: ¿cómo determinar el valor de Eu si fuera necesario estimar, por ejemplo, asentamiento a corto plazo en arcillas? Nuevamente, en base a lo establecido por la Teoría de la Elasticidad. Tal como señalan Lambe & Whitman (1969) en su obra clásica sobre Mecánica de Suelos, la relación entre el módulo de deformación E para diferentes condiciones de drenaje viene dada por:
Eu = 1,15E´
Respecto a esta relación, los mencionados autores advierten que para suelos particularmente blandos, de elevada deformabilidad, esta relación puede alcanzar valores de 3 o 4, lo que implica que los asentamientos estarían gobernados por la deformación a largo plazo, como efectivamente ocurre en suelos susceptibles de consolidar.
¿Por qué emplear el módulo G en análisis de asentamientos de cimentaciones?
Para contestar esta pregunta, primeramente es necesario reconocer que existe una suerte de barrera en muchos profesionales de la Ingeniería Geotécnica, quienes consideran que, tal como ha ocurrido históricamente, el módulo G es válido únicamente para análisis dinámicos. Sin embargo, sólo es necesario echar un vistazo a las secciones anteriores, o al elevado nivel de conocimiento que hemos alcanzado sobre el tema a lo largo de los últimos 50 años (en este punto, considero que las referencias de Jardine et al, 1985; Atkinson, 2000; Oztoprack & Bolton, 2013; y Vardanega & Bolton, 2013; Cox & Mayne, 2015 – que les dejo al final del post – pueden ser de gran utilidad para profundizar en el tema), para comprender que no es el caso.
De hecho, el empleo del módulo G en la estimación de asentamientos (siguiendo el proceso descrito someramente en la sección 2 de este post) tiene la ventaja de que los módulos de deformación obtenidos, resultan más cercanos a los módulos de deformación in situ. Esto podemos verlo en la Figura 3 que les muestro a continuación.
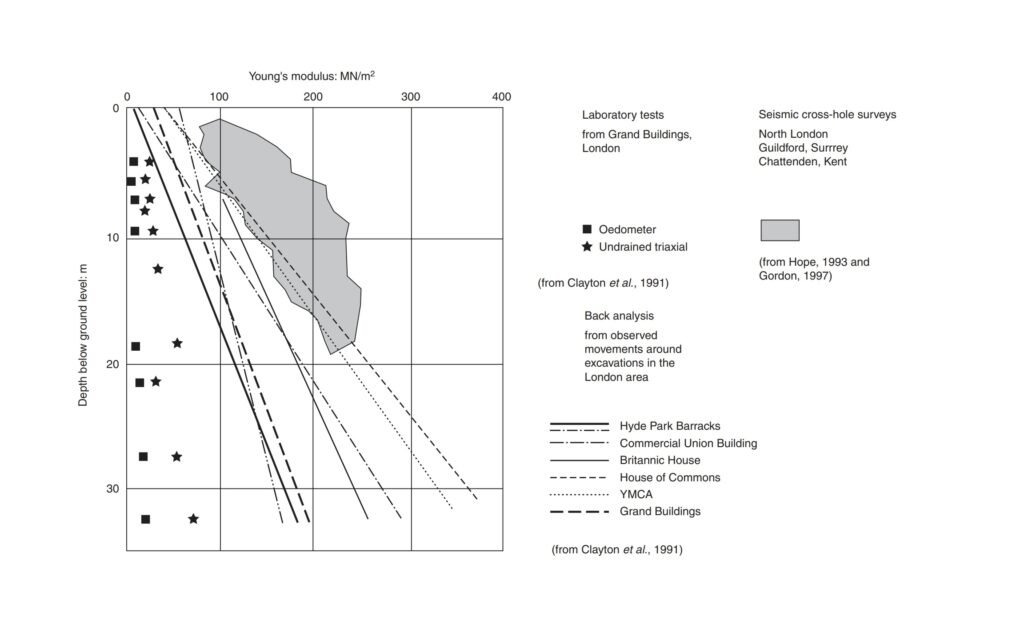
Figura 3 Perfiles de rigidez para varios terrenos ubicados en Londres, UK (Fuente: modificado de Simons & Menzies, 1999).
En esta gráfica vemos claramente la relación entre los módulos de deformación Eu obtenidos a partir de: 1) ensayos de laboratorio convencionales; 2) back-análisis a partir de mediciones de movimientos de las estructuras; y 3) ensayos geofísicos.
Así, en base a lo ilustrado en esta figura, considero oportuno destacar dos hechos fundamentales:
- Que los ensayos de laboratorio subestiman de manera importante los valores de módulo de deformación respecto a las condiciones in situ.
- Que los ensayos geofísicos permiten obtener el valor de Go, a partir del cual es posible estimar G para cada análisis en particular.
De acuerdo a lo anterior, es evidente que el empleo del módulo de corte G como parámetro fundamental para la estimación de asentamientos de cimentaciones bajo solicitaciones estáticas, proporciona una mejor aproximación a la estimación real de la rigidez del terreno, lo que, a su vez, permite optimizar el diseño de la cimentación.
Referencias
- Atkinson, J. (2007) “The Mechanics of Soils and Foundations”. Second Edition. CRC Press – Taylor & Francis Group. Abingdon, UK.
- Atkinson, J. H. (2000) “No-lineal Soil Stiffness in Routine Design”. Geotechnique 50, No. 5, 487-508.
- Cox, C. & Mayne, P. (2015) “Soil Stiffness Constitutive Model Parameters for Geotechnical Problems: A Dilatometer Testing Approach”. Third Conference on DMT, no. 12. Rome, Italy.
- Jardine, R.; Fourie, A.; Maswoswe, J. & Burland, J. (1985) “Field and Laboratory Measurements of Soil Stiffness”. Proceedings of the Eleventh International Conference on Soil Mechanics and Foundation Engineering, pp. 511-514. San Francisco, USA.
- Mitchell, J.K. & Soga, K. (2005) “Fundamentals of Soil Behavior”. Third Edition. John Wiley & Sons, Inc. New Jersey, USA.
- Oztoprack, S. & Bolton, M. (2013) “Stiffness of Sands through a Laboratory Test Database”. Geotechnique 63, No. 1, 54–70 (http://dx.doi.org/10.1680/geot.10.P.078).
- Simons, N. & Menzies, B. (2000) “A Short Course in Foundations Engineering”. 2nd. Edition. Thomas Teldford Limited 2000. London, UK.
- Vardanega, P. & Bolton, M. (2013) “Stiffness of Clays and Silts: Normalizing Shear Modulus and Shear Strain”. Journal of Geotechnical and Geoenvironmental Engineering, Vol. 139, No. 9. ©ASCE, ISSN 1090-0241/2013/9-1575–1589.