The blog of Alvaro Boiero
"Live as if you were going to die tomorrow. Learn as if you were going to live forever" Mahatma Gandhi
The blog of Alvaro Boiero
geo
"Live as if you were going to die tomorrow. Learn as if you were going to live forever" Mahatma Gandhi
Lateral earth pressure: the ka condition
The rest condition Ko occurs only if no movements of the wall are generated. If a rotational or translational deformation occurs around its base, the stress state of the ground in the extrados of the wall changes, generating the condition of active thrust KA. Do you want to know more? Continue reading this post…
Content
The active thrust condition
Displacements occurring in a wall influence the in situ stress state of the soil around the wall. During the installation of the wall, and as translational and/or rotational movements are generated at its base, the earth pressures change from the original Ko condition to active and passive stress states, depending on the relaxation behind or compression in the lower front zone of the wall, respectively.
The amount of horizontal movement that the wall must experience at its top to reach the active state, depends on the type of soil and the height of the structure (H), as shown in Table 1.
Table 1 Movement of the wall to reach the active condition (Source: Coduto, 2001).
Type of soil | Horizontal movement required to reach the active condition |
Dense sand | 0,001 H |
Loose sand | 0,004 H |
Hard clay | 0,010 H |
Soft clay | 0,020 H |
H = height of the wall.
Earth pressures generated by the active state behind the retaining structure will significantly influence the bending moments, shear forces, and any supporting shoring forces.
Estimation of coefficient Ka
How to estimate the Ka coefficient, necessary to analyze the stress state at the back of the wall? Traditionally, this parameter has been estimated in terms of effective stresses. This approach applies for all soils, and for any moment in the life cycle of the structure, but implies that the approximate distribution of pore pressures must be known in order to estimate the effective stresses (Powrie, 2012).
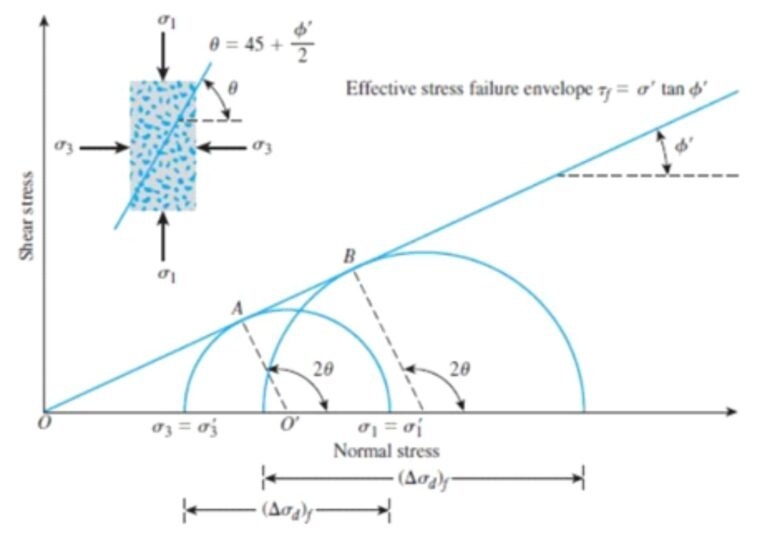
Figure 1 Mohr circle of effective stresses (Source: Karkush, 2018).
Assuming vertical and horizontal directions for the principal stresses, for an active thrust state to be reached, the stress conditions must be such that the largest principal stress is vertical, and the smallest principal stress is horizontal. Thus, it is satisfied that the minimum horizontal stress is given by:
In this equation, Ka is the active horizontal pressure coefficient, which is determined from the following expression:
As can be seen, this coefficient is expressed as a function of the effective angle of internal friction of the soil.
Service conditions
One of the important aspects to highlight, is that the real walls are not free of friction, so the existence of shear forces in their back or front part would invalidate the assumption that the directions of the principal forces are vertical and horizontal, as we saw in the previous section.
For this reason, modern design codes (e.g. EUROCODE 7) consider the influence of wall-earth friction by means of the angle δ. Figure 2 shows schematically the typical design conditions of a retaining wall, as established in the current design codes.
Figure 2 Design conditions for a retaining wall (Source: available at https://slideplayer.com/slide/12944312/).
It should be noted that the aforementioned codes require the design to be carried out considering the ultimate limit state (ULS), which implies the reduction of the actual soil resistance, either through a factor of safety or through a resistance mobilization factor (Powrie, 2012).
Accordingly, the "factored" soil resistance will result in an increase of the earth pressure coefficient Ka. Furthermore, if δ = 0 is considered, the value of Ka is higher and, therefore, the design would be more conservative, which would give the project an acceptable safety margin.
We have already reviewed the basic notions of the state of rest and the state of active thrust. In a next post we will deal with the passive thrust state, in order to close the topic of lateral earth thrust coefficients, which are fundamental for the design of retaining walls.
References
- Coduto, D. (2001) “Foundation Design: Principles and Practices”. Second Edition. Prentice Hall. New Jersey, USA.
- Karkush, M. (2018) “Soil Mechanics”. University of Baghdad – Department of Civil Engineering. Available at https://www.researchgate.net/profile/Mahdi-Karkush.
- Powrie, W. (2012) “Earth Pressure Theory”. Chapter 20 ICE Manual of Geotechnical Engineering. Insitution of Civil Engineers. London, UK.
