

Application of IS units in geotechnical engineering
Every time we have reviewed a text on Geotechnical Engineering, Soil Mechanics, or any other branch of Engineering, especially some of the older ones, we have encountered the dilemma of units. Depending on the origin of the work, some present all the analyses and results in English units, others in the so-called "MKS" system, mixed with the old "CGS", and all accommodated to the multiples and submultiples used in practice. A great confusion that, fortunately, the International System of Units (II) has helped to unify.
Content
Measurements in Geotechnical Engineering
There has always been some confusion about the appropriate system of units for physical quantities and measurements. And that confusion has been increasing with the growth of international cooperation and trade, i.e., globalization. Thus, it became evident that a single system of units, accepted throughout the world, is not only convenient, but tremendously practical. Why?
Holtz et al (2011) provide an excellent answer to this question. Engineers and laboratory technicians, as in any other physical science, traditionally use the CGS (centimeter - gram - second) system in routine laboratory measurements. They also apply the MKS (meter - kilogram - second) system for pressure and stress measurements in triaxial tests, and the British System for compaction tests. This is an accepted practice that, in general, causes great confusion for novices in this branch of engineering.
One of the main sources of confusion, even from the point of view of physical understanding of the properties being measured in the laboratory or field, is the use of force as a basic unit. Mass should be the basic unit, and force a derived unit, applying Newton's well-known Second Law (F = ma). The use of the kilogram as a unit of force is one of the difficulties of the "metric system" (yes! another system that accompanies the MKS and CGS!), which is a modified version of the MKS, traditionally employed in Europe and Latin America. This system, as many readers will know and have experienced, distinguishes mass from force by including the adjective "force" to the unit: thus, in the "metric system", if you have kilogram it is mass; but if the term kilogram-force appears, it is a force. Really very confusing and, moreover, impractical.
Taking into consideration this diverse situation regarding units, around 1960, the "International System of Units" (Le Systeme International d'Unités) was adopted by the General Conference on Weights and Measures (CGPM), in order to unify the use of units, not only in Geotechnical Engineering, but also in science and commerce in general.
So let's get to know the International System (IS), and particularly how it is applied in Geotechnical Engineering and Soil Mechanics.
The International System of Units (IS)
The International System of Units (IS) is based on seven basic units, namely:

Figure 1 Basic units of IS.
Each of the basic units shown in Figure 1 has certain peculiarities: 1) they have a precise definition; 2) name and symbols; 3) units for all other physical quantities can be derived from them.
The main advantage of the IS is that one, and only one, unit exists for each physical quantity, and all other mechanical quantities (such as velocity, force, and work, for example) can be derived from these basic units. In addition, the IS units of force, energy and power are independent of the nature of the physical processes, whether mechanical, electrical or chemical.
An additional advantage of the IS is that it is a fully coherent system, where coherence is to be understood in the special sense of a system whose units are mutually related by rules of multiplication and division with no numerical factor other than 1 (BIPM, 2000).
The IS has other important features: the use of unique and well-defined abbreviations and symbols, and a convenient decimal relationship between multiples and submultiples of the basic units.
As can be seen, there are many advantages offered by the IS. Let's review it a little more in depth, considering the units usually used in Geotechnics and Soil Mechanics.
Units of interest in Geotechnical Engineering
The units of interest in Geotechnical Engineering are length, mass, time and, for some lab applications, temperature.
As mentioned above, each of these units has precise physical definitions, as shown in Figure 2.
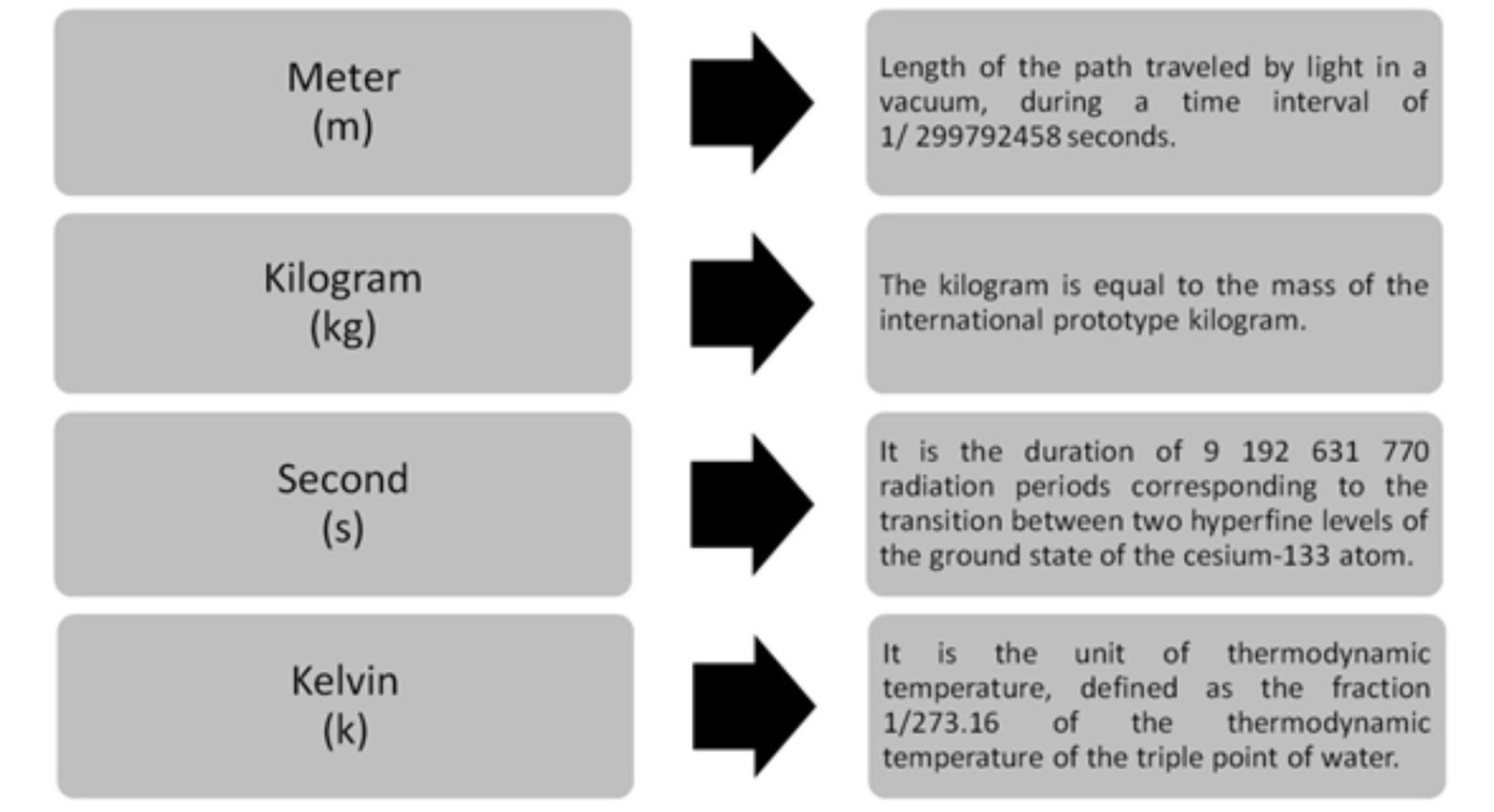
Figure 2 Definitios of units of interest in Geotechnical Engineering.
Let's look at some interesting information about these definitions, as to better understand the importance and the analyses associated with them over the years, to finally arrive at them, as summarized by the Bureau International des Poids et Mesures - BIPM (2000):
- • The 1889 definition of the meter, based on the international platinum-iridium prototype, was replaced by the 11th CGPM (1960), using a definition based on the wavelength of krypton-86 radiation. In turn, it was replaced by the current one (see Figure 2) in 1983 by the 17th GFCM.
- • The international prototype of the kilogram, made of platinum-iridium, is maintained in the BIPM under the conditions specified by the 1st CGPM in 1889 (CR, 34-38), which sanctioned that the prototype represented the unit of mass. The 3rd CGPM (1901, CR, 70), in a statement intended to end the ambiguity in the popular use of the word "weight", confirmed that the kilogram is the unit of mass, and which presents the definition that it still maintains today
- The unit of time, the second, was at one time considered to be the 1/86400 fraction of the mean solar day. The exact definition of the mean solar day was based on astronomical theories. However, numerous measurements showed that there were irregularities in the rotation of the Earth, which could not be explained by the theory, which had the effect that this definition could not achieve the required level of accuracy. Considering that a very precise definition of the unit of time is indispensable for the International System, the 13th GFCM (1967 - 1968, Resolution 1; CR 103 and Metrology, 1968, 4, 43) adopted the definition of the second shown in Figure 2. In 1997, it was established that this definition refers to a cesium atom at rest at the temperature of 0 K.
- The definition of the thermodynamic temperature unit was essentially given by the 10th CGPM (1954, Resolution 3; CR, 79), which chose the triple point of water as the fundamental fixed point and assigned to it the temperature 273.16 K, thus defining the unit, as shown in Figure 2. The unit of Celsius temperature is the degree Celsius, symbol °C, which is by definition equal in magnitude to the kelvin. A temperature difference or range can be expressed in kelvins or in degrees Celsius. The numerical value of a Celsius temperature expressed in degrees Celsius is given by the well-known relationship:
T/°C = T/K – 273,15.
On the other hand, it is worth recalling here the derived units commonly used in Geotechnical Engineering, as well as the prefixes used to indicate multiples and submultiples of the basic and derived units. Tables 1 and 2, taken from Holtz (1980), summarize the derived units and prefixes in common use, respectively
Table 1 Derived units used in Geotechnical Engineering (Source: Holtz, 1980).

Table 2 Prefixes to indicate multiples and submultiples (Source: Holtz, 1980).

Knowing the above definitions and their physical meaning, the following sections present conversion factors useful in the practice of Geotechnical Engineering.
Conversion Factors
This section summarizes the conversion factors usually used in practice, and includes some comments on the use of IS units.
These conversion factors, as well as those for many other physical units, are available at https://www.convertworld.com/es/.
Length
The most common conversion factors for British and MKS systems are as follows:
1 inch, in = 25,4 mm = 0,0254 m
1 foot, ft = 0,3048 m
1 yard, yd = 0,9144 m
1 mile = 1,609 x 103 m = 1,609 km
1 nautic mile = 1,852 x 103 m = 1,852 km
1 angstrom, Å = 1 x 10-10 m = 0,1 nm
1 mil = 2,54 x 10-5 m = 0,0254 mm = 25,4 μm
Good practice using IS suggests that multiples and submultiples of units of length be used in increments of 1000, e.g. mm, m, km.
Mass
Mass, as some of you may remember from your Physics classes, is an appropriate measure of the amount of matter contained in an object. Mass remains constant, even when the temperature, shape, or some other physical attribute of the object changes. Unlike weight, the mass of an object does not depend on local gravitational attraction, so it is independent of the object's location in the Universe.
Some useful conversion factors related to mass measurements are as follows:
1 mass-pound, lbm = 0,4536 kg
1 short-ton, ton = 2000 lbm = 907,2 kg
1 gram, g = 1 x 10-3 kg
1 metric ton, t = 1 x 103 kg = 1 x 106 g = 1 Mg
1 slug (1 lb-fuerza/ft/s2) = 14,59 kg
The kilogram is the only IS unit whose name, for historical reasons, contains a prefix.
Time
In practice, although the second is the basic IS unit of time, minutes (min), hours (h), or days (d) can be used whenever convenient, even if these units are not decimally related.
Force
As can be seen in Table 1, force is a derived unit in the IS, from the well-known Newton's Second Law F = Ma. Its unit is the newton (N), which is equal to 1 kg∙m/s2.
The most common conversion factors are summarized below:
1 force-pound, lbf = 4,448 N
1 short-ton-force, ton-force = 8,896 x 103 N = 8,896 kN
1 kg-force = 1 kp = 9,807 N
1 kilopound – force, kip = 1000 lbf = 4,448 x 103 N = 4,448 kN
1 metric-ton force, t-force = 1000 kp = 9,807 x 103 N = 9,807 kN
1 dina (g∙cm/s2) = 1 x 10-5 N = 10 μN
In practice, it is more convenient to express quantities as multiples of the newton. Thus, the commonly used prefixes are kilo, mega and giga (see Table 2), so that forces are usually expressed in kilonewtons (kN), meganewtons (MN), or giganewtons (GN).
A very common force in every geotechnical engineering problem is weight. According to what we have seen so far, considering Newton's Second Law, weight must be expressed in newtons.
Another problem related to weight is that the term is commonly used when in fact it refers to the mass of an object. For example, when someone "weighs" an object on a laboratory balance, they are really comparing two masses: the unknown mass of a certain object with a known mass. Further ambiguity, if possible, occurs when some units of mass, such as kilogram or pound, are used as units of force (Holtz et al, 2011).
Thus, considering the above, and also taking into account that weight depends on the acceleration of gravity (which varies with latitude and altitude), the IS recommends the use of mass.
Stress and Pressure
In the IS, the unit used to measure stress and pressure is the pascal (Pa), which is derived by relating the units of force and area, being equal to 1 newton per square meter (1 N/m2).
Some common conversion factors:
1 force-pound/square inch, psi = 6,895 x 103 Pa = 6,895 kPa
1 kg-force/cm2 = 9,807 x 104 Pa = 98,07 kPa
1 kg-fuerza/cm2 = 9,807 x 104 Pa = 98,07 kPa
1 t-force/m2 = 9,807 x 103 Pa = 9,807 kPa
1 bar = 1 x 105 Pa = 100 kPa
1 ksi (kip/in2) = 6,895 x 106 Pa = 6,895 MPa
1 lb-force/ft2 = 47,88 Pa
The Pascal is obviously a small unit. But using IS it is easy to add prefixes to make larger numbers more manageable. For example, for routine triaxial testing, the cell pressure is usually variable between 200 psi and 300 psi, which is equivalent to 1379 kPa and 2068 kPa, respectively. These quantities are much more easily expressed in megapascals: 1.5 MPa and 2.0 MPa, respectively.
¿Density or Unit Weight?
It is very common in Geotechnical Engineering the confusion between density and unit weight. Why? There are many reasons, but there are two of special importance:
- I. The confusion in relation to the measurement that a balance yields. As mentioned earlier in this post, any balance basically performs a comparison of masses. Therefore, what any balance measures is mass (not weight). On this topic, you can check https://www.ingmecafenix.com/medicion/balanza/, o bien https://sciencing.com/tools-used-measure-mass-5305130.html.
- II. The use of other systems, such as the MKS or the "metric system", commonly used in Europe and some Latin American countries.
Density is defined as mass per unit volume. In the IS, density has units of kilogram per cubic meter (kg/m3), although it is sometimes expressed in megagrams per cubic meter (Mg/m3).
The most common conversion factors are as follows:
1 mass-pound/cubic foot, lb-mass/ft3 = 16,018 kg/m3
1 g/cm3 = 1 x 103 kg/m3 = 1 Mg/m3 = 1 t/m3
It is good to remember that the density of water (ρω), is exactly 1000 g/cm3 at a temperature of 4°C, and that the variation of this value in the range of usual temperatures in Geotechnical Engineering, is small. Therefore, the error associated with the use of this value for ρω is sufficiently accurate in practical applications.
Unit weight, on the other hand, is defined as weight per unit volume, and is commonly measured and used in practical geotechnical engineering. However, the ASTM (American Society for Testing and Materials) recommends using density instead of unit weight, because density represents a constant value that does not depend on the variation of the acceleration of gravity.
In any case, the important thing is to know the difference between density and unit weight. Although the differences are obvious and they are two different physical quantities, it is a very common mistake for many engineering professionals to confuse the two terms. So let's review the theory well and remember a bit of high school physics classes!
References
- Holtz, R., Kovacs, W. & Sheahan, T. (2011) “An Introduction to Geotechnical Engineering”. Second Edition. Pearson, USA.
- Holtz, R. (1980) “SI Units in Geotechnical Engineering”. Geotechnical Testing Journal, GTJODJ, Vol. 3, No. 2, pp.73-79.
- Bureau International des Poids et Mesures (2000) “El Sistema Internacional de Unidades SI”. Traducción realizada por Cogno, J.A. y Steinberg, R.