"If you can't explain it simply, you don't understand it well enough" (Albert Einstein)
geo
"If you can't explain it simply, you don't understand it well enough" (Albert Einstein)
Equivalent fluid method (EFM) for estimating lateral thrust on a wall
Equivalent fluid pressure (EFP) is a simplification of the lateral load exerted by soil on a retaining wall. This equivalent fluid refers to a hypothetical fluid, of unit weight such that it produces a pressure against a lateral support whose value is approximately that which would be produced by a real soil. Do you want to learn more about this topic? Continue reading the post...
Content
Equivalent fluid method (EFM) for estimating earth pressure
In general, it is possible to assume that the theoretical distribution of lateral earth pressure generated by a granular backfill on a wall is triangular in shape (Coduto, 2001). This is the same shape that would be assumed for the case of a wall that is loaded by a fluid instead of soil. Accordingly, if such a fluid had the appropriate unit weight, the magnitude of the lateral pressure exerted on the wall would be equal to that of the pressure exerted by the soil. This is the basic idea of the equivalent fluid method (EFM).
The EFM has its origin in the document Standard Specifications for Highway Bridges, published by the American Association of State Highway Officials in USA around the 1950s. This document stated that all earth retaining structures should be designed to withstand a minimum pressure generated by a fluid of unit weight equal to 30 pcf (4.9 kN/m3). However, this method of pressure and retaining wall analysis has been scrutinized over the years to validate its applicability in design, resulting in a series of typical equivalent fluid unit weight values to be used in practical problems. These typical values are shown later in this post.
Rankine and Coulumb equations in the framework of the EFM
According to this approach, engineers and designers can then apply the idea implicit in the EFM. Thus, instead of estimating values of the lateral earth pressure coefficient K (if active, passive or at rest), it is possible to describe earth thrust using the equivalent fluid unit weight Gh, corresponding, as mentioned above, to a fictitious fluid that would impose a thrust level on a wall equivalent to that exerted by the soil. The vertical component of earth pressure, Gv, can also be expressed through the EFM.
In that way, the normal and shear forces acting on a wall can be expressed as shown in Figure 1.
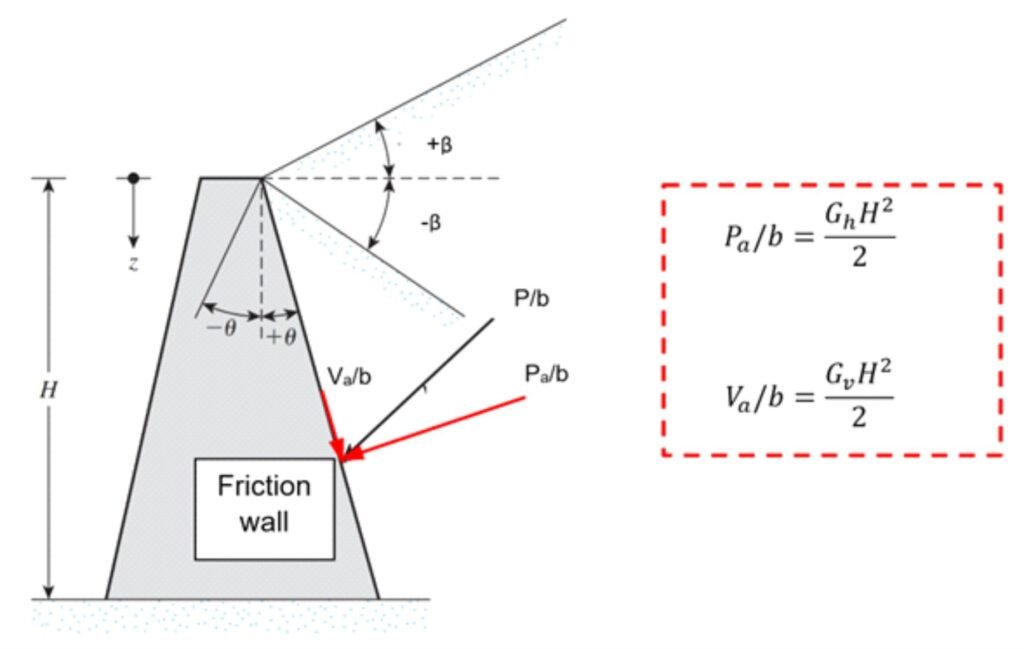
Figure 1 Determintion of normal and shear forces acting on a wall using the EFM.
In the figure above: Pa/b = normal force acting between backfill and wall per unit wall length; Va/b = shear force between backfill and wall per unit wall length; Gh, Gv = equivalent fluid unit weights in the horizontal and vertical directions; H = wall height; β = backfill inclination.
On the other hand, considering the expressions for estimating the normal and shear forces acting on the back of a wall with granular backfill with zero cohesion (i.e. c = 0), it is possible to express the equivalent unit weights as a function of the lateral earth thrust coefficients proposed according to Rankine and Coulomb theories as follows (Coduto, 2001):
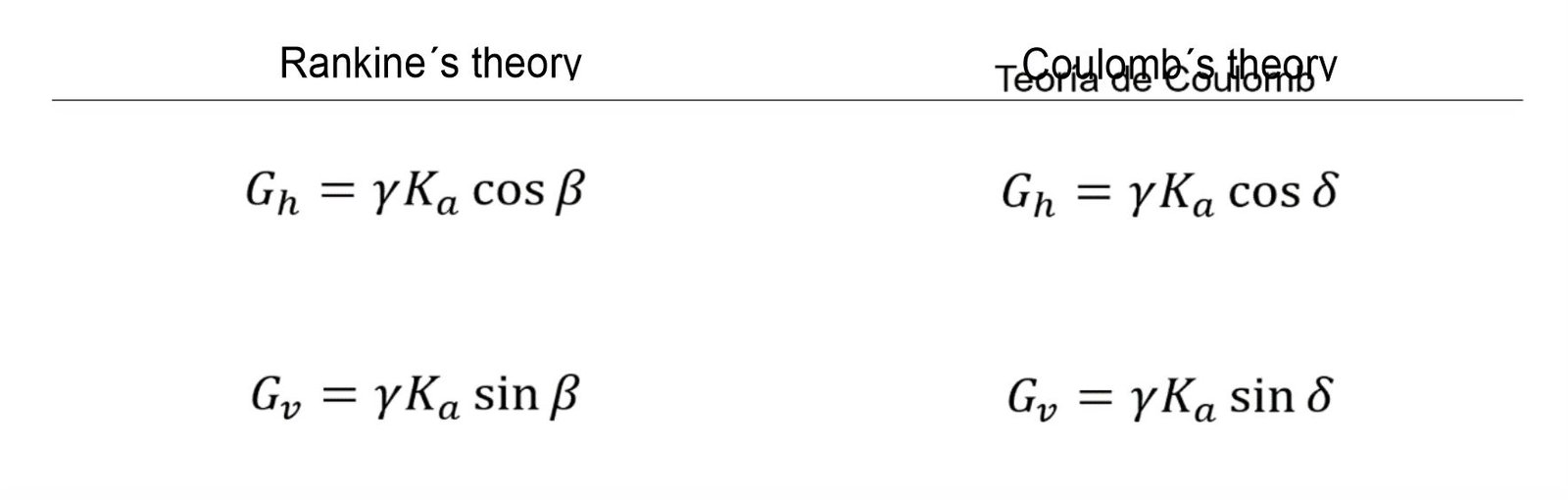
Where: γ = unit weight of soil; Ka = active coefficient of earth thrust determined from Rankine's or Coulomb's theory; β = inclination of the backfill at the back of the wall; δ = angle of friction at the soil-wall interface.
Thus, knowing the unit weight and the angle of internal friction of the backfill, and the angle of inclination of the wall, it is possible to estimate the values of the unit weight of the equivalent fluid, considering either the Rankine or the Coulomb approach, depending on the designer's preferences.
Earth thrust values according to the EFM to be used in design
Table 1 shows estimated values of the equivalent unit weight Gh for different types of granular soils, both for the active case and for the resting state (i.e., under Ko conditions). According to Coduto (2001), the active pressure values can be used for cantilever walls, while the resting pressure values can be used for braced walls. In any case, the height of the wall should not exceed 2.5 m.
Table 1 Equivalent unit weight values for different types of granular materials and maximum wall height H = 2.5 m (Source: Coduto, 2001).
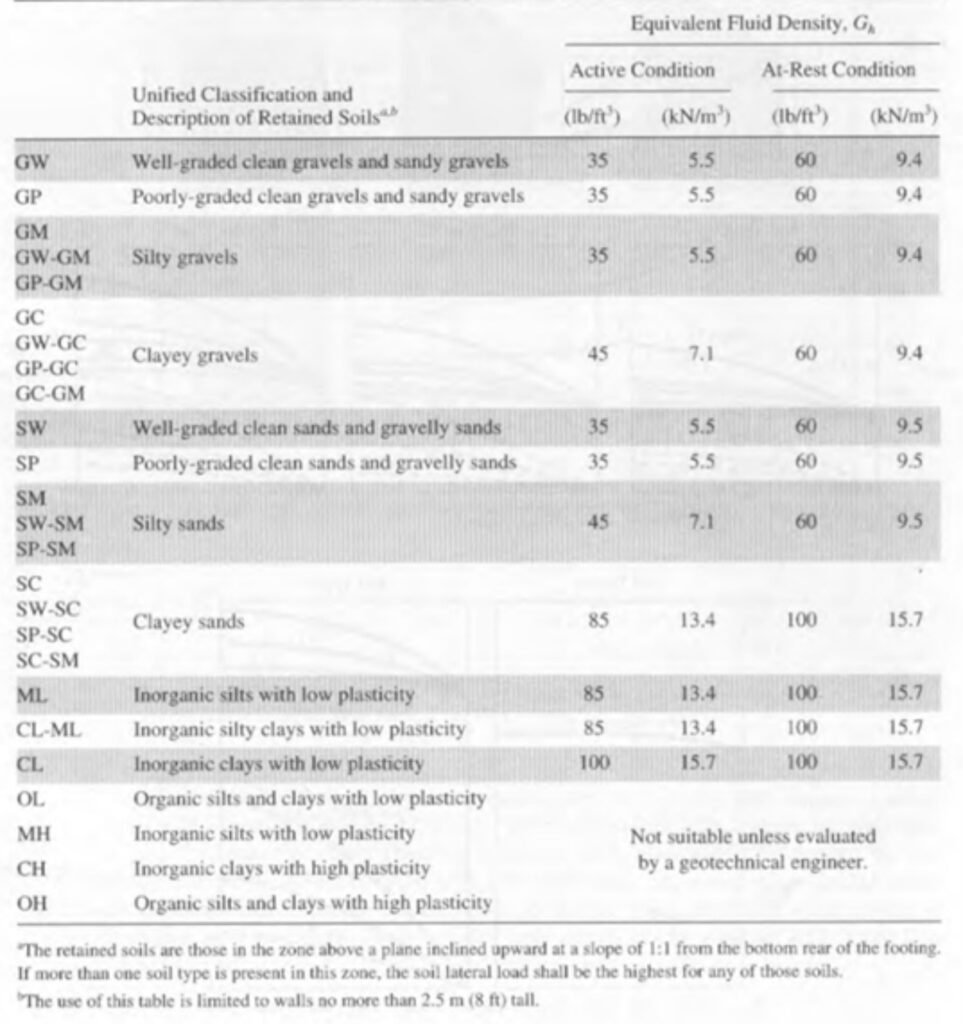
As conclusion, it is worth mentioning that, based on the approach outlined here, Geotechnical Engineers can develop equivalent fluid unit weight design values for different types of granular fills, and subsequently present them to the Structural Engineer, who can perform the design by applying the principles of fluid statics.
References
- Coduto, D. (2001) “Foundation Design: Principles and Practices”. Second Edition. Prentice Hall. New Jersey, USA.
- O´Rourke, T. & Jones, C. (1990) “Overview of Earth Retention Systems”. Proceeding Paper. Part of Design and Performance of Earth Retaining Structures. Ithaca, New York, USA.
